磁気共鳴映像法(MRI)の原理
|
はじめに 核磁気共鳴(NMR, Nuclear Magnetic Resonance)について、我われは、原理上、主磁場 B0 の強度(磁束密度 [T テスラ])が高ければ高いほど、検出される信号強度も高いことを知っている。そのために、我われは、MRI装置として磁場強度が高い、高価なものを購入する。しかし、主磁場の強度と信号強度の関係は、未知の定数を含んだ比例式で表されることが多い。これが等式で表されることを知る人は少ない。ここでは、「信号強度」を等式で提供する。 「炭素 13(C-13)」は、原子核としてプロトン「6個」と中性子「7個」をもっている。よって、「炭素 13(C-13)」には「水素(H-1)」の約「13倍」の質量がある。主磁場 B0 の強度(磁束密度)が同じであるとき、「炭素 13(C-13)」の原子核の歳差運動の速度は、「水素(H-1)」の歳差運動の速度の約「4分の 1」である。原子核は、この速度が低ければ低いほど、「信号強度」も低い。「炭素 13(C-13)」の「信号強度」は、「水素(H-1)」の約「1.59パーセント」である。リン(P-31)やフッ素(F-19)など、他の幾つかの種類の原子核についても、「信号強度」のそのような比較表が多く作成されて知られている。しかし、我われが実験的に感知できるのは「検出感度」、すなわち、「信号強度」を「雑音強度」で割った「信号雑音比」にほかならない。「雑音強度」も、原子核の回転速度が低ければ低いほど、低い。ここでは、「雑音強度」と「検出感度(信号雑音比)」を、いずれも等式で提供する。 以上が、国内外の書籍などにない本書の特徴である。また、本書は、以下、可能な限り古典物理学を用いて述べる。これによって、読者は「何」が起きているか、基本に立ち帰って考えることができるはずである。 なお、次のリンクも参考になれば幸いである。 『磁気共鳴映像法(MRI)の原理』(直感的に「あぁ、そうだったのか」と理解するためのビジュアル・コンテンツ) https://www.asoshiranui.net/mriliteracy/『磁気共鳴映像法(MRI)の科学略史』 https://www.asoshiranui.net/mrihistory/【1】 原子核の歳差運動 自然界に存在する多くの原子核のうち、「陽子」(水素原子核、プロトン)の数と「中性子」(n、ニュートロン)の数の少なくとも一方が奇数である原子核は、核磁気共鳴(NMR)を起こす。水素原子核(プロトン)は、「1H」または「H-1」と表記される。水素原子核は、これを「正の電荷をもつ超高速の回転体」と見なしてよい。これはさしあたり正しい。この回転体は「スピン」と呼ばれることがある。もっとも「スピン」は、本来は「回転する」という意味の動詞である。 原子核の回転は、「点」が回転しているわけではない。ある形をもった「物体」が回転軸の周りを回転する。その物体は「角運動量」という物理量をもっている。「角運動量」は回転の勢いを表す物理量である。物体の回転軸から離れた部分は大きく回転しているわけであり、角運動量は大きい。回転軸に近い部分は同じ速度で小さく回転しているわけであり、角運動量は小さい。位置 r において、運動量 p を持つ質点の回転軸まわりの角運動量 L は L = r×p で定義される。ここで「×」は「外積」である。回転する一つの物体がもつ角運動量は、その物体の各部がもつ角運動量を合計して(積分して)求められる。 原子核がもつ角運動量は「スピン角運動量」L(spin angular momentum)とよばれる。水素原子核では、 L = √{I(I + 1)}
h /(2π) 古典力学(ニュートン力学)では、質量 m [Kg]、半径 a [m] の均質な球体が周期 T [s] で回転するとき、角運動量の大きさは L = 4πm a2/(5T) [Kgm2/s] である(「剛体の力学」の教科書を参照)。この [Kgm2/s] という単位は前記の [Js] と同一である。 プロトンの質量は、およそ m = 1.7×10-27 [Kg] である。また、プロトンを仮に密度が一様な球体と仮定したときに、その半径はおよそ a = 8.0×10-16 [m] である。すると、プロトンのスピン角運動量 L = 4πm a2/(5T) の値が前記の 9.2×10-35 だというわけである。ここで、T は、回転の「周期」、すなわち、「一回転するのに何秒かかるか」であり、回転速度 n(ニュー)の逆数である。よって、プロトンを「回転する正の電荷」と見なすとき、1秒間あたりの自転速度 n (= 1/T)の数値は、 n = 3.4×1022 [1/s] であることが分かる。これは、想像を絶する高速であるが、古典物理学では、このようなことになるわけである。 プロトンは、正電荷 1.6×10-19 クーロン [C] をもっている。この正電荷が回転する軌道半径 r は、プロトンを一様な球体と見なした場合よりもやや大きく、r = 1.2×10-15 [m] である。プロトンはその回転によってアンペールの右ねじが進む向きに磁界を放つ。図は、仮に z 方向の静磁場として磁束密度 B0 [T] の中に一個のプロトン(グレー色の球)がおかれたとして、歳差運動の様子をイメージ化したものである。 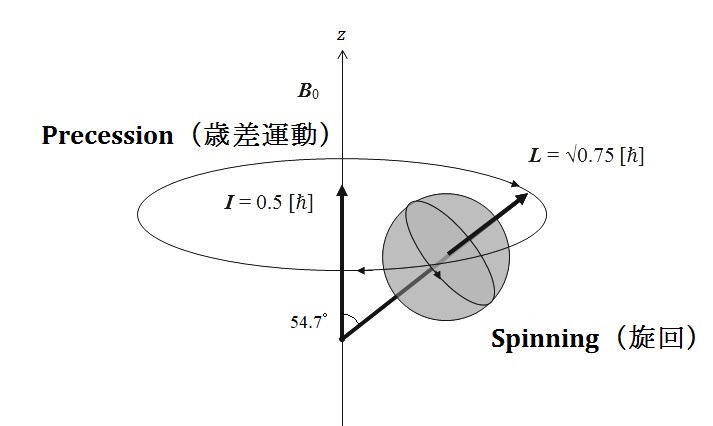 静磁場(磁束密度 B0)の中におかれた一個のプロトン
スピン量子数 I とは、スピン角運動量 L の主磁場(z 方向)の成分にほかならない。スピン量子数 I とスピン角運動量 L は、二辺が 0.5 [ℏ] と √0.75 [ℏ] の直角三角形がもつ 54.7°の角度をなしている。プロトンの歳差運動に伴って角運動量 L の向きは時々刻々と変わるが、中心軸 z の向きのスピン量子数 I は大きさも向きも不変である。
プロトンを磁束密度 B0 [T] の静磁場におくと、歳差運動の速度 ω0 は「磁気回転比」γ を定数として磁束密度 B0 に比例する。この比例関係は「ラーモアの法則」として知られている。 ω0 =γB0 [rad/s] 以下、プロトンの歳差運動について、この「ラーモアの法則」が成り立つことを確認しておく。先ず、一つの円周に沿って電荷 e[C]が 1秒間に n0 [Hz] の回転数で回っていると仮定する。電荷は円周を 1秒間に e n0[C]の量だけ移動する。1秒間に移動する電荷の量とは電流 i[A]のことであるから、円周に流れる電流は、円の大きさによらず i = e /T [A] と表される。プロトンがもつ電荷量は e = 1.6×10-19 [C] であり、回転速度(回転の周波数)は前記したように n0 = 3.4×1022 [1/s] であるから、 i = 5.4×103 [A] プロトン(1H)の「赤道」にはこのように 5,400 [A] もの大きな電流が流れていることになる。半径 r[m]の円環に i[A]の電流を流すとき、円環の中心の磁界は、磁束密度 B = μ0 i /(2r) [T] である(「電磁気学」の教科書を参照)。μ0 は「真空透磁率」4π10-7 [H/m] である。半径を r = 1.2×10-15 [m] としたので、プロトン 1個の中心を貫く磁束密度は約「3兆テスラ」であることが分かる。そのようにプロトンは「微小にしてかつ強大な磁石」ということになる。微小な円環は、面積 S = πr2 [m2] を囲んでいる。その円環に電流 i[A]が流れるとき、それによって生じる磁気モーメントの大きさは(「電磁気学」の教科書を参照)、 i S = iπr2 [Am2] その磁束密度 B0 方向の成分μの大きさは、μ = i S cosθ [Am2] プロトンについて、このμの大きさは i = 5.4×103 [A]、S = π(1.2×10-15)2 [m2]、θ = 54.7°として、μ = 1.41×10-26[Am2]である。この面積 S について、電流の向きに対して右ネジの進む向きに大きさ S の「面積ベクトル」を考えると、磁気モーメントは、i S としてベクトルで表わされる(「電磁気学」の教科書を参照)。この磁気モーメント i S に対して磁束密度 B0 によって生じる偶力のモーメント N は、 N = i S × B0 角運動量の方程式は(「電磁気学」の教科書を参照)、 dL / dt = N L sinθ・ω0 dt = i S B0 sinθ dt ω0 = (i S cosθ B0)/ I [rad/s] ω0 =γB0 [rad/s] (ラーモアの法則) プロトン(1H)の磁気回転比 γ は、スピン磁気量子数 I = 1/2(h/2π)、プランクの定数 h = 6.63×10-34 [Js] であるから、γ = 26.75×107 [rad/(sT)] である。プロトン以外の原子核についても、古典的な同様の計算で磁気回転比 γ を求めることができる。 核磁気共鳴を起こす原子核には中性子の数が奇数のものもある。中性子は正味の電荷を持たないが、磁気モーメントをもっている。この一見矛盾する中性子の性質について、湯川理論によれば中性子はある時間は陽子と負の「中間子」に解離していると仮定され、このとき中間子の磁気モーメントは陽子とは符号が逆であると考えられている。 【2】 巨視的磁化 生体組織 1グラムの中にはおよそ 1023 個のプロトン(水素原子核)が存在する。個々のプロトンの磁気モーメントの方向は通常ばらばらであるので、外部から磁気的な性質があることはわからない。しかし、生体組織を静磁場の中に置くと、個々のスピンは静磁場と同じ向きの「αスピン」と逆の向きの「βスピン」とに分離する。αスピンとβスピンの数の割合はマックスウェル・ボルツマンの「気体分子に関する速度分布の法則」に従って、αスピンの数の方がβスピンの数よりもわずかに多く、そのわずかの差によって、生体組織には「巨視的磁化 M0」が現われる。これは大きさと向きをもつベクトル量である。一個の原子核に着目してみると、静磁場がないときは方向が不確定であるが、磁束密度 B0 が存在してはじめてスピン磁気量子数 I が磁束密度 B0 の方向に一致する。磁気モーメント μ は、 μ = γI I の単位は「h /(2π)」である。ここで、h = 6.63×10-34 [Js](プランクの定数)、I を無名数として μ = γ{h /(2π)} I と表してよい。磁気モーメントの z 軸成分である μ と磁束密度B0 の相互作用は「ハミルトニアン H 」で表わされる。 H = - μ∙B0 ハミルトニアン H の固有値は「ゼーマンレベル」といわれるポテンシャル・エネルギー E である。E = -γ (1/2π) I B0 プロトンでは、I の値としては、磁束密度 B0 と同じ向きの「αスピン」の I = 1/2 と、逆向きの「βスピン」の I = - 1/2 の二つの状態が存在する。エネルギーとして低い状態にある αスピンの方が、エネルギーとして高いレベルにある βスピンの数よりもごくわずかに大きい。それぞれに対応するゼーマンレベル(ポテンシャル・エネルギー)は、Eα = - (1/2) γ (h /2π) B0 ⊿E = γ (h /2π) B0 αスピンがエネルギー ⊿E によって反転して βスピンに遷移する過程を、我々はそのまま直感的に理解することはできない。ただ直感的に理解できることは、αスピンも βスピンも原点から見て右回りに(すなわち時計回りに)自転し、したがって、それぞれのスピン角運動量ベクトル L の先端にいずれも N極がある微小な磁石とみなせることと、αスピンは、原点から見て左回りに歳差運動を行ない、βスピンは、原点から見て右回りに歳差運動を行なうために、αスピンもβスピンも主磁場の S極から見れば、いずれも右回りに歳差運動を行なうことと、したがって、αスピンも スピンも、共通の「回転座標系」で見ると、両方とも静止して見ることができるということである。このことのために我われは量子力学的な現象である磁気共鳴をなお古典物理学的な手段を用いてかなりよく理解できるという幸運に恵まれている。絶対温度 T [K] の下で気体分子の集団は、運動エネルギー E = (1/2)mv2 をもつ分子の数が exp(- E/kT )に比例することが知られている(マックスウェル・ボルツマンの気体分子に関する速度分布の法則)。ここで k はボルツマンの定数 k =1.38×10-23 [J/K] である。プロトンについても αスピンの数と βスピンの数がこの法則に従い、その結果、Nβ と Nα の比は次の式で表わされる。 Nβ /Nα = exp{(- ∆E /(kT)} ここで - ∆E /kT = hν0 /kT の実際の値は、たとえば、磁気共鳴の周波数 f0 = 750MHz、サンプルの絶対温度が 277 K(4℃)としても、約1.3×10-4であり、極めて小さな値である。関数 ex は、x の値が極めて小さい場合には ex = 1 + x として極めて正確に近似されるので、Nβ /Nα = 1 - ∆E /(kT) また、Nα + Nβ = N(サンプルの単位体積あたりのスピンの総数)とすると、Nα - Nβ = γ(h /2π)B0 N /(2kT) プロトンは、たとえばサンプルの温度 37℃ で静磁場の磁束密度 1 [T] では、(Nα- Nβ )/N = 2.77×10-6 であるから、全体の約 36 万分の 1 のスピンが磁束密度 B0 と同じ向きの αスピンとして巨視的磁化ベクトル M0 を形成する。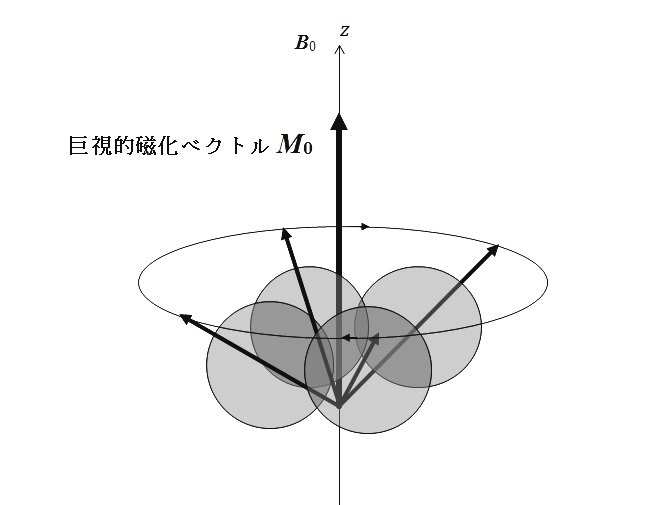 スピン 4個でつくられた巨視的磁化ベクトル M0
個々のαスピンは歳差運動のどの位相をもつかは分からないが、図では何億個ものαスピンを 4 個で代表させて表している。個々の αスピンの歳差運動は位相が時々刻々と変化するが、巨視的磁化ベクトル M0 は一つの大きさと、主磁場 B0 と同じ向きをもっている。
サンプルの単位体積あたりの磁気モーメントの大きさ M0 は、 M0 = μ (Nα - Nβ ) M0 = γ2 (h /2π)2 B0 I(I + 1)N /(3kT) このM0 がサンプルの単位体積あたりの巨視的磁化の大きさである。M0 の磁束密度B0 に対する係数は、サンプル全体の「磁化率」χm として知られている。M0 = χm B0 ここで、常磁性体の磁化率 M0 が絶対温度 T に反比例することは「ピエール・キュリーの法則」として知られている。【3】 ファラデーの誘導起電力(EMF, Electromotive Force) 巨視的磁化ベクトル M0 に対してスピンの歳差運動と同じ角周波数 ω0 をもつ磁束密度 B1 cosωt [T] の RF磁界を x 軸方向に Δt [s] の時間だけ加える。すると、スピンは x 軸のまわりに(z 軸のまわりでなく)θ = γB1Δt [rad] で表わされる位相角θだけ「歳差運動」を行なう。回転座標系では 高周波の RF磁界 B1 cosωt がスピンによって経験される唯一の「静磁場」であるからである。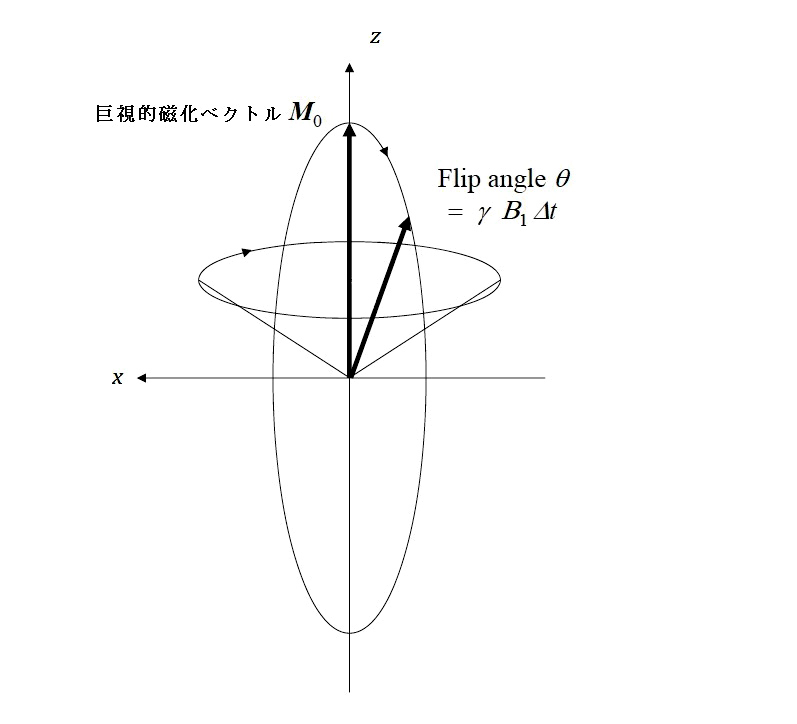 RF磁界によってつくられるフリップ角 θ
すなわち、RF磁界 B1 cosωtを加えると、個々のスピンは、歳差運動の軸として z 方向を保っているが、巨視的磁化ベクトル M0 は xy 平面上に角度 θ = γB1 [rad] だけ連続的に倒れていく。
「RFコイル」は、導電体(金属)でできた共振コイルである。「フリップ角θ」とは RF磁場 B1 に対する巨視的磁化 M0 の歳差運動の「位相」のことである。これは 20°であることもあり、90°であることも 180°であることも 270°であることもあり得る。 たとえば、フリップ角 θ が 90°である場合に(図)、個々のスピンの歳差運動の軸の方向は z 軸の向きであれ逆向きであれ、依然として z 軸の方向に保たれている。図では四つのスピンのうち二つのスピンがαスピンであり、残りの二つのスピンがβスピンとして主磁場の方向 z に垂直な巨視的磁化ベクトル M0を形成している様子を表す。これは RF磁界として二つのスピンをβスピンに「励起」するだけの電力量(電力×時間)を加えた結果である。RF磁界の電力量はパルス状に加えられることが多く、図は「90°パルス」を加えた直後の様子であるといえる。仮に 90°パルスの二倍の電力量を「180°パルス」として加えていたなら、四つのスピンはすべてβスピンとなり、巨視的磁化ベクトル M0は図の下向き(-z 向き)となっていたであろう。 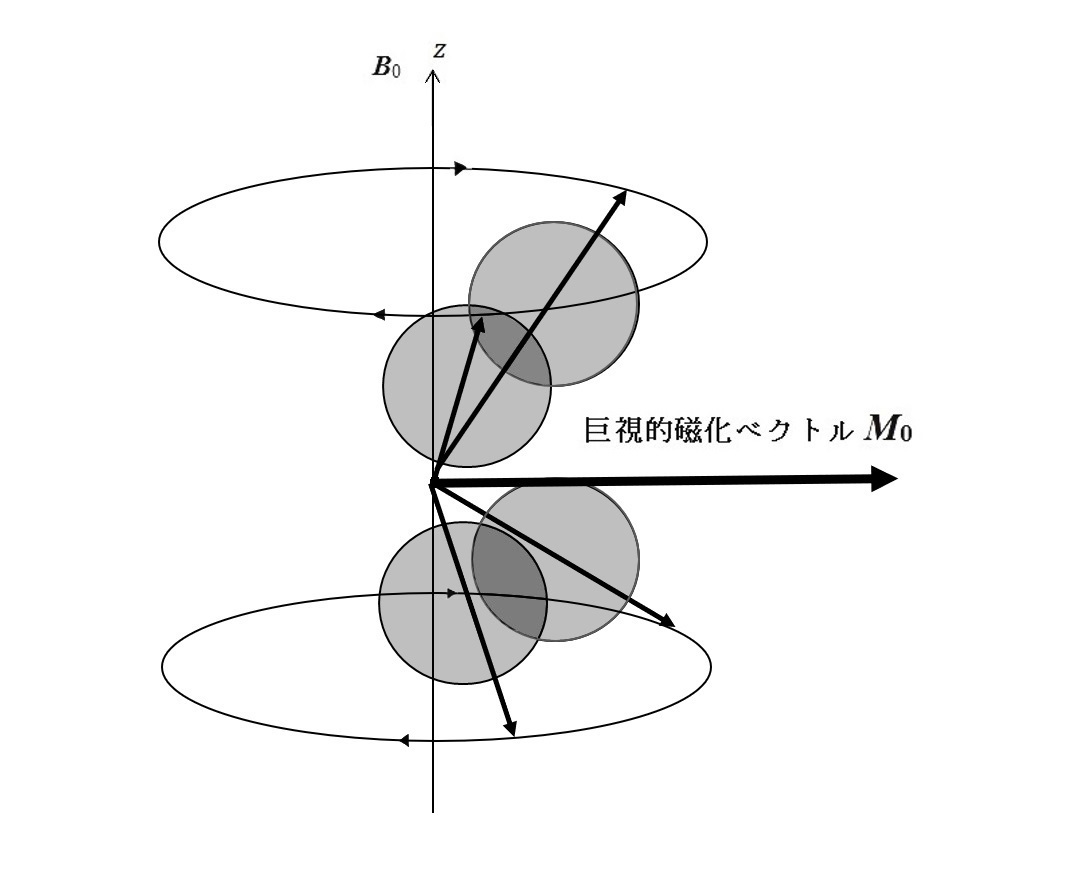 静磁場の方向 z に対して 90°倒れた巨視的磁化ベクトル M0 【4】 雑音強度 試料は、たとえば人体や生理食塩水など、一般に導電性をもっている。磁束が試料を貫通しようとすると、逆向きに「対抗磁束」が発生する。このとき試料の内部には渦電流が発生している。この対抗磁束はコイル自身の「電気抵抗」として RFコイルがもつ純抵抗に加算される。RFコイルによって試料に RF電力 P を供給すると、コイルに流れる電流 i* はi* = (P/R)1/2 である。ここで R は RFコイルの総抵抗(RFコイルの純抵抗と、対抗磁束によって RFコイルに加算される電気抵抗の合計値)である。単位電流をもつコイルが発生する磁束密度を B1 とすると、試料に加わる磁束密度はB1* = B1(P/R)1/2 となる。RFコイルの B1 値はもともと RFコイルの幾何学的な寸法・形状によって設計可能である。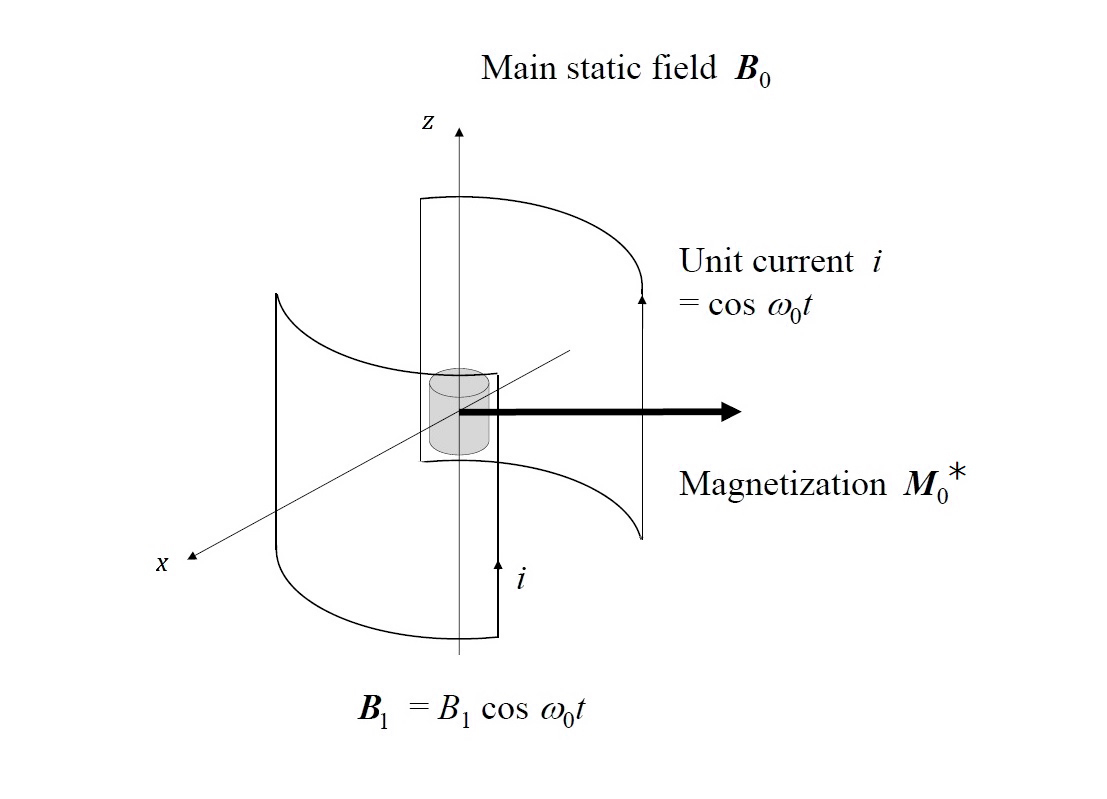 RF磁束密度 B1 図は、単位電流 i = cosω0t が流れるコイルから発生する RF磁場(B1 cosω0t)によって、フリップ角θが 90°になったときの試料の関心領域(VOI, volume of interest)の巨視的磁化 M0* を示す。RFコイルからの電力をオフにしても、巨視的磁化 M0* はベクトルとしてしばらくは RFコイルと鎖交した(RFコイルを貫通した)ままであるから、RFコイルにはファラデーの誘導起電力 ξs が生じる。 ξs = - d(B1×M0*)/ dt RF磁界は B1 cosω0t であるからξs = ω0B1M0* sinω0t 関心領域 VOI の原子核の数は N* = 103 c v A である。ここで A はアボガドロ数(6.02×1023)、v は VOI の体積(m3)、c は原子核の濃度(M)であるから、M0* = 103 c v A γ2 (h/2π)2 B0 I (I + 1) /(3 k T) ここで h はプランクの定数、I はスピン量子数、k はボルツマン定数、T は絶対温度(K)である。原子核の濃度 c、RF磁場 B1、関心領域 VOIの体積 v が決まれば、他の定数はすべて既知の値であるから、ファラデーの起電力 EMF ξs の値は理論的に定まる。出力であるファラデーの起電力 ξs は多くの場合にマイクロボルト(μV)のレベルである。現在の MRI製造各社の出力値は、この理論的な数値に近い。起電力 ξs はプリアンプ(前置増幅器)によってミリボルトのレベルに増幅される。 【5】 共鳴の緩和 試料に 90°の RFパルスを加えると、αスピンの半数が励起されてβスピンとなる。180°パルスを加えるとαスピンの全数が励起されてβスピンとなる。励起された原子核をそのままにしておくと、エネルギーをだんだん失って低エネルギーの安定な αスピンに戻る。これは「縦緩和」または慣用的に「T1 緩和」と呼ばれる。T1 緩和は指数関数的な変化であり、T1 はその時定数である。T1 緩和は巨視的な現象として、dMz /dt = (M0 - Mz )/T1 と表され、ここで Mz は磁化の z 軸成分である。例えば、人の脳の白質のプロトンの T1 値は、典型的には 690 [ms] である。固体のように分子の動きが制限されていると、T1 緩和はほとんど起こらず、T1 値は数時間にも及ぶことがある。原子核は大きな分子の構成要素であることが多く、T1 値は分子の構造を反映する。原子核は、北極と南極を持つ小さな磁石として互いに影響し合っている。ここで、一つの原子核が実際に経験する静磁場の磁束密度 B0 は、他の原子核の存在によって変化する。そのため、同じ静磁場 B0に置かれた原子核は、少しずつ異なる周波数の歳差運動を行い、それらの歳差運動の位相はそろわなくなっていく。これは「横緩和」または慣用的に「T2 緩和」と呼ばれる。T2 緩和も指数関数的な変化であり、T2 はその時定数である。T2 緩和は巨視的な現象として、dMxy /dt = - Mxy /T2 と表され、ここで Mxy は磁化の z 軸に垂直な xy 平面上の成分である。T2 緩和によって起電力 ξs の振幅は指数関数的にだんだん小さくなり、自由誘導減衰 (FID, Free Induction Decay) を示す。 ξs = ξs0 exp (iω0t) exp(- t/T2) 振幅の初期値ξs0 は、ξs0 = ω0 B1 M0* である。 T1 緩和とは対照的に、T2 緩和におけるエネルギーの交換は原子核の間だけで行われる。例えば、人の脳の白質のプロトンの T2 値は、典型的には 110 [ms] である。大きな分子の原子核の T2 値は一般に短い。また、低分子でも高分子に結合すると T2 値も短くなる。例えば、抗がん剤のフルオロウラシル溶液は鋭い 19F 共鳴ピークを示し、T2 値は 200 [ms] より長いが、肝細胞に取り込まれると T2 値は 10 [ms] より短くなる。 静磁場 B0 が不均一な場合にも、原子核の歳差運動の位相はそろわない。その時に起きる信号の減衰は緩和のように見えて「T2スター(T2 *)緩和」と呼ばれる。「シミング」といって静磁場の磁束密度 B0 の均一性を高める作業によって T2* 値を長くすることができる。不均一な静磁場に置かれた原子核からの FID信号 ξs は、次のように表される。 ξs = ξs0 exp (iω0t)exp (-t/T2* ) 原子核が 90°パルスで励起された後、xy 平面上の磁化のベクトル M0は T2* 緩和によって振幅が指数関数的にだんだん小さくなる。しかし、直後に180°の RFパルスが続くと、ばらばらとなりつつあった位相は再収束して原子核はエコー信号を発生する [Hahn, 1950]。これがスピン・エコー(SE)信号である。180°パルスは原子核の歳差運動の位相をあたかも時間が逆転したかのように再収束させるため、しばしば「時間反転のパルス」と呼ばれる。 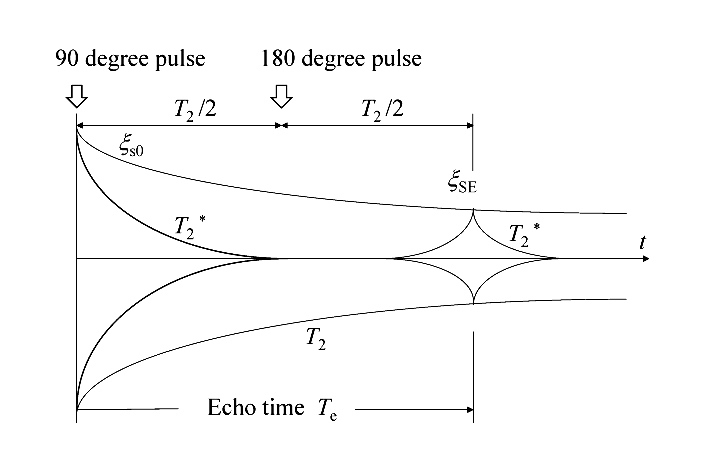
スピン・エコー(SE)信号 ξSE の発生 スピン・エコー信号の振幅 ξSE は、繰り返し時間 Tr の間は T1 緩和の影響を受け、エコー時間 Te の間は T2 緩和の影響を受ける。ξSE は次のように表すことができる。 ξSE = ξs0 {1- exp(-Tr /T1)}exp (-Te /T2) したがって、スピン・エコー信号 ξs は、次のように表すことができる。 ξs = ξs0 {1- exp(-Tr /T1)} exp(-Te /T2) exp(iω0t)exp(- |t - Te|/T2*) スピン・エコー信号 ξs は、エコー時間 Te に対して振幅は対称になる。励起パルスとリフォーカス(再収束)パルスを 90°、180°ではなく、それぞれ θ1、2θ2 とすると、スピン・エコー信号ξs は次のように表される。 ξs = ξs0{1- exp(-Tr/T1)} exp(-Te/T2)exp(iω0t)exp (- |t - Te|/T2*)sinθ1 sin2θ2 【6】 「スピン・ワープ(spin warp)イメージング」の概要 静磁場である磁束密度 B0 の空間は、身体の三つの解剖学的な平面(横断面・冠状断面・矢上断面)に対応する三つの交差する平面をもっている。それらの平面は、いずれも「傾斜磁場」といって空間的な位置によって磁束密度が異なる「静磁場」を加えることによって特定される。傾斜磁場は「勾配磁場」ともいわれる。勾配磁場は傾斜磁場コイルによって生成される [Turner, 1993]。勾配磁場は直交する三方向(x、y、z)のそれぞれについて線形の傾斜磁場をつくり出すように構成されている。傾斜磁場コイルは二組のコイルに互いに逆向きの電流を流すことによって勾配磁場をつくり出す。「z方向の傾斜磁場・Gz」は、静磁場の中心点から +z の向きに離れる距離に比例して +z 向きの磁束密度が高い。「x方向の傾斜磁場Gz」は、静磁場の中心点から +x の向きに離れる距離に比例して(+x 向きでなく) +z 向きの磁束密度が高い。スライス選択は、勾配磁場と共鳴励起のための RF磁場パルスを同時に印加することによって行われる。また、スライス面に直角な第二の方向と第三の方向の原子核の存在密度と緩和のふるまいも、傾斜磁場によってその位置が特定される。「スピン・ワープ・イメージング法」は、フィールド・エコー(FE)イメージング、スピン・エコー(SE)イメージング、エコー・プレイナー・イメージング(EPI)などの撮像方法の基本的な原理をなしている [Hutchison et al.,1980; Edelstein et al., 1980]。 【7】 第一の方向(z 軸の方向)の「スライス選択」 試料(ヒト頭部)を静磁場 B0 に置いて、第一の方向(z 軸の方向)の傾斜磁場 Gz を加えると、試料の中の原子核は、磁束密度が核磁気共鳴周波数 ω0 に固有の領域でのみ RF磁場によって励起される。これは試料をスライス選択して行われる原子核の共鳴励起であり、スライス選択は傾斜磁場 Gz の z 軸方向で行われる。RF励起のパワーを変調することによってスライス選択のプロファイルを決めることができる。sinc関数、すなわち(sint)/t のエンベロープ(包絡線)関数をもつ励起パワーは矩型の形状(プロファイル)をもつ励起を与える。ガウス型エンベロープ関数を持つ励起パワーはガウス型のプロファイルをもつ励起を与える。励起の有効周波数帯域幅は、加えた RFパルスの有効時間の逆数である。励起パルスが sincのエンベロープ関数で、メインローブの半値幅が 1 [ms] の場合、得られるスライスは帯域幅が約 1 [kHz] の矩形のプロファイルとなる。励起時間が長いほど、得られるスライスの厚さは薄くなる。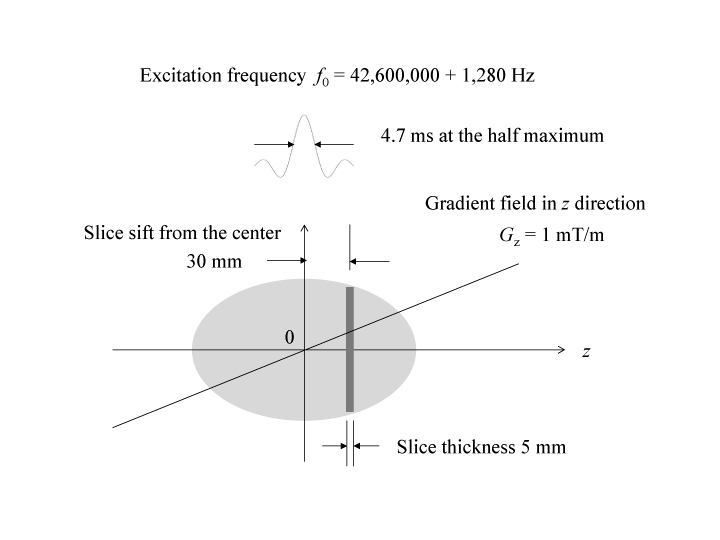
傾斜磁場によるスライス選択 プロトンの共鳴周波数は約 42,600,000 [Hz/T] であるため、図に示すように傾斜磁場が 1 [mT/m] の場合、共鳴周波数を 42.6 [Hz/mm] に分布させることができる。メインローブの sincエンベロープとして半値幅 4.7 [ms] のパルスを印加すると、フーリエ変換された帯域幅は 213 [Hz] になる。したがって、厚さ 5 [mm]の矩型のスライスが励起される。RFパルスの周波数をf0 = 42,600,000 + 1,280 [Hz] とすると、スライス選択の位置は +z 軸方向に 30 [mm] ずれることになる。 【8】 第二の方向(x 軸方向)に分布する原子核からの信号の位置の認識 第二の方向、すなわち x 軸方向に分布する原子核からの信号の位置の認識は、信号を取得するときにx 軸方向の傾斜磁場 Gx を印加することによって行う。傾斜磁場 Gx によって、x 軸の方向に分布する原子核の共鳴周波数は、低周波数から高周波数へ x 軸の方向に線形に分布する。例えば、傾斜磁場 Gx が 1 [mT/m] の場合に、x 軸の方向に -0.1 [m]〜 +0.1 [m] の領域では、共振周波数は -4,260 [Hz] から +4,260 [Hz] まで線形に分布することとなる。この周波数の帯域幅は、通常のコンピューターで処理できるほど小さい。 RF共振コイルで取得した信号(ファラデーの誘導起電力)は、x 軸方向に分布する原子核の位置に応じた周波数をもち、フーリエ変換によってその分布が復元される。これが x 軸方向の原子核の位置の「符号化」であり、単に「信号の読み出し」(reading out)と呼ばれる。フーリエ変換によって、試料の x 軸方向への「投影曲線」が得られる。投影曲線のデータは、「直交復調」(quadrature demodulation)によって検出された実数値 Re と虚数値 Im 、及び絶対値 √(Re2 + Im 2)で表示される。例えば、取得データ点数が 512点で、その半分が実数、残りが虚数であれば、256点の折れ線グラフで絶対値の投影曲線を表示することになる。 「読み出し傾斜磁場」Gx を加えると、原子核の歳差運動の周波数が x 軸方向に分布するようになり、それぞれの位相は急速にばらばらとなって取得される信号強度は急速に減衰する。この減衰は、負の(ディフェイジングの)傾斜磁場 -Gxd を加えておいて、正の傾斜磁場 +Gx に反転させることで回復させることができる。これによって、フィールド・エコー(FE)信号が生成される。 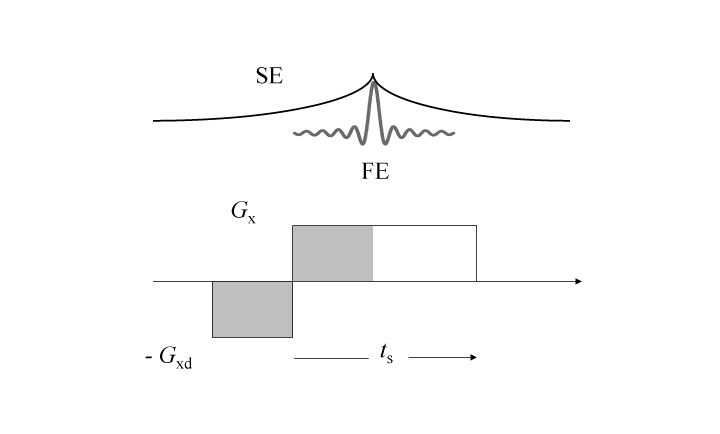
読み出し傾斜磁場の反転とフィールド・エコー(FE)信号 図に示すように、フィールド・エコー(FE)信号が発生するのは、グレーの部分の面積(傾斜磁場の強度×時間)が同じになるタイミングである。傾斜磁場 Gx が 1 [mT/m] の場合に、傾斜磁場 Gx によって発生するプロトン周波数の偏差は、x 軸方向に 42,600 [Hz/m] となる。MR画像の視野(FOV, field of view)が例えば x 軸方向に 30 [cm] とすると、それをカバーする周波数帯域幅は 12,800 [Hz] となる。「サンプリングの定理」によれば、AD変換器のサンプリングレートは 25,600 [Hz] 以上でなければならない。 スピン・エコー(SE)イメージングでは、180°パルスで発生する SE信号と、読み出し傾斜磁場 Gx を反転させて発生する FE信号を合成して取得する。すなわち、SEのリフォーカス(再収束)の瞬間とFEのリフォーカスの瞬間を一致させる。  t(s) t(s)
フィールド・エコー(FE)信号  f(Hz) f(Hz)
フーリエ変換されたフィールド・エコー(FE)信号の実数値 Re  f(Hz) f(Hz)
フーリエ変換されたフィールド・エコー(FE)信号の絶対値 Av = √(Re2 + Im 2) 図は実際に時間 ts の間に取得されたエコー信号の一例である。横軸は時間(秒)である。また、そのエコー信号をフーリエ変換した結果として信号データの実数値 Re 及び絶対値 Av = √(Re2 + Im 2)を図示する。横軸は周波数(Hz)である。実数値の図は立体的な螺旋(らせん)形の平面図であると見てよい。虚数値(図示しない)はその立面図となるが、一見するだけでは、同じ立体的ならせん形の立面図であるから、実数値の図とほとんど変わらない。絶対値 Av の曲線は、実数値 Re または虚数値 Re の曲線の包絡線(エンベロープ)の形状に近い。 【9】 第三の方向(y 軸方向)に分布する原子核からの信号の位置の認識 第三の方向に分布する原子核からの信号の位置の認識は「位相エンコーディング」によって行われる。これは図のようにスライス選択励起の後に開始される。典型的なフィールド・エコー(FE)撮像シーケンスは、図に示すように、z 軸方向のスライス選択励起と x 軸方向の周波数エンコード、y 軸方向の位相エンコードの組み合わせである。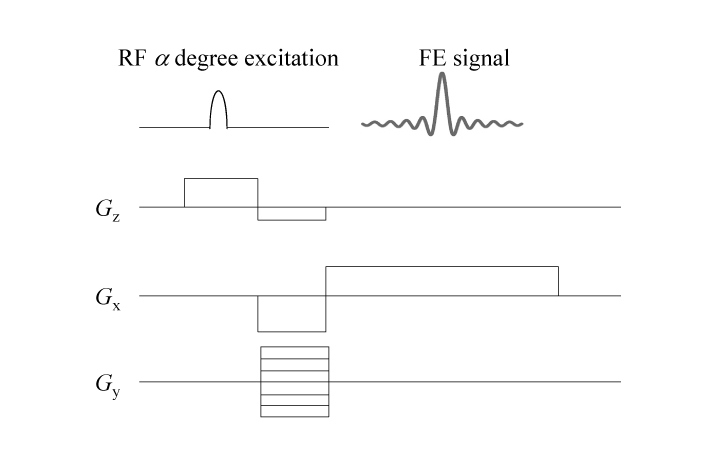
フィールド・エコー(FE)撮像シーケンス スライス選択は傾斜磁場 Gz を加えるのと同時に RF励起パルスを加えて行われる。励起終了後(RFパルスを加えて後)も傾斜磁場 Gz を冗長に加え続けると、選択されたスライスの表と裏とでは励起された原子核の歳差運動の速度が異なるので、歳差運動の位相がばらばらとなる。最終的に一本の共振コイルで原子核からの共鳴信号を取得するには位相はそろっている(コヒーレントである)ことが必要である。反転傾斜磁場 -Gz を加えることによって、スライスの中でばらばらとなった歳差運動の位相を巻き戻しておく。 先ず、小さな傾斜磁場 Gy を一定時間 Δt だけ加える。すると、原点(y = 0)から +y 方向に離れた位置にある原子核は、原点にある原子核よりも高い静磁場を受けることになる。一定時間Δt が経つと原点(y = 0)から +y 方向に離れた位置にある原子核の歳差運動の位相は、原点にある原子核のそれよりも大きい。一方、原点(y = 0)から -y 方向に離れた位置にある原子核は、原点にある原子核よりも低い静磁場を受けることになる。一定時間Δt が経つと原点(y = 0)から -y 方向に離れた位置にある原子核の歳差運動の位相は、原点にある原子核のそれよりも小さい(マイナスの向きに大きい)。 次に、二回目のスライス選択励起の後に傾斜が二倍大きい(磁束密度の空間変化率が二倍大きい)傾斜磁場 Gy を同じ y軸方向に同じ一定時間Δt だけ加える。更に、三回目のスライス選択励起の後に傾斜が三倍大きい傾斜磁場 Gy を同じ y 軸方向に同じ一定時間Δt だけ加える。このようにして、傾斜磁場 Gy の大きさを段階的に変化させて、例えば、256回のステップで加える。これによって、原点から遠い位置にある原子核ほど、傾斜磁場 Gy の大きな変化を受ける。したがって、原子核は、その一定時間 Δt 毎に歳差運動の位相に大きな変化を経験する。 取得した 256個のデータセットをフーリエ変換することによって、原子核が原点から y 軸の方向にどれだけ離れているかが認識される。 図は、x方向と y方向について二次元フーリエ変換した結果を模式的に表すものであり、横二つ・縦二つの四ピクセル(画素)からなる MR画像を表している。 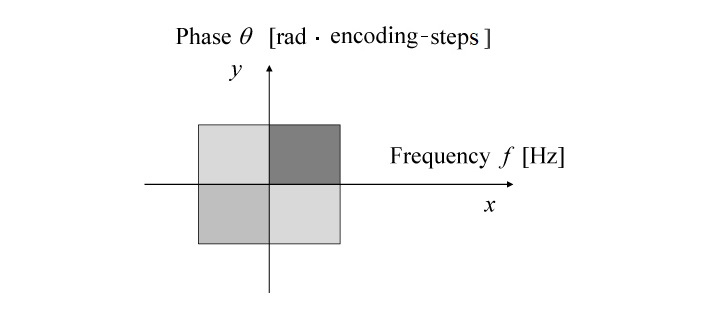
横(x 軸)が周波数軸であり、縦(y 軸)が位相軸である平面 傾斜磁場 Gy の大きさを 256回、例えば -2.54 [mT/m] から +2.56 [mT/m] まで 0.02 [mT/m] のステップで変化させると、y 軸方向の原点から 10 [cm] 離れた位置にある水素原子核は、静磁場の磁束密度が 0.002 [mT] ずつ変化し、共鳴周波数は 85.2 [Hz] ずつ 256回変化する。例えば 一定時間 Δt が 3 [ms] の場合、原点から 10 [cm] 離れた位置では、歳差運動の位相が毎回 2π・85.2・0.003 = 1.6 [rad] だけ 256回変化する。フーリエ変換することによって y 軸の方向に分布する原子核からの信号の位置が認識される。 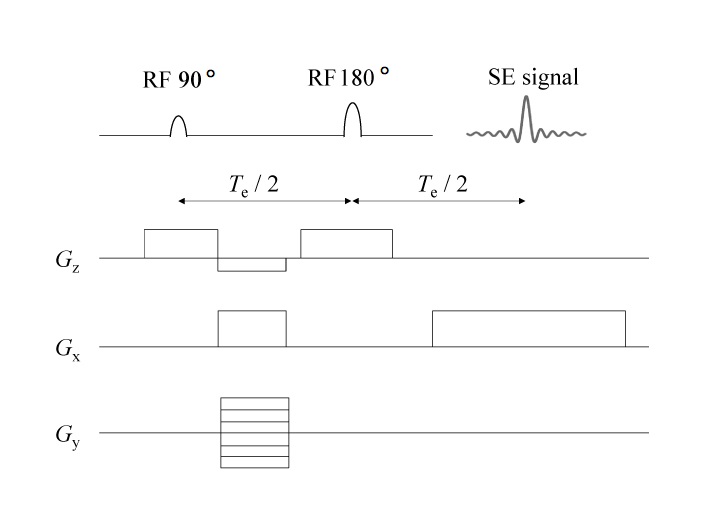
スピン・エコー(SE)撮像シーケンス スピン・エコー(SE)イメージング・シーケンスにおいて 180°パルスは、90°パルスによる選択励起の後、Te/2(s)経過したところで加えられる。これによって「エコー時間」Te でスピン・エコー(SE)信号が取得される。 なお、180°パルスを加える時にスライス選択傾斜磁場 Gz を加えてよい。特定のスライスの中にある原子核だけに反転の 180°パルスが加わることになる。また、負の傾斜磁場 -Gxd を加えておいて、正の傾斜磁場 +Gx に反転させる代わりに、180°パルスを加えるよりも前のタイミングで正の傾斜磁場 +Gxd を加えてもよく、これによってフィールド・エコー(FE)信号も生成される。 【10】 k - スペース 取得されたエコー信号データは、伝統的に「k -スペース」と呼ばれる平面上に順番に並べられる [Ljunggren, 1983]。
取得した実数値データ Re を k - スペース上に順番に並べたもの プロトンは静磁場の磁束密度が 1 [T] 以上である場合に NMR信号は 42,577,479 [Hz] 以上の周波数をもっているわけであるが、この「中心周波数」は差し引かれる。前記したように、例えば、傾斜磁場 Gx が 1 [mT/m] の場合に、x 軸の方向に -0.1 [m] 〜 +0.1 [m] の領域では、共振周波数は -4,260 [Hz] から +4,260 [Hz] まで線形に分布していて、この周波数の帯域幅は、通常のコンピューターで処理できるほど小さい。 取得されたエコー信号データは、異なる周波数を含む波に見える。エコー信号も「直交復調」によって検出されており、実数値 Re と虚数値 Im をもっている。エコー信号の実数値データの図も立体的な螺旋(らせん)図形の平面図であると見てよい。虚数値(図示しない)はその立面図となるが、一見するだけでは実数値の図とほとんど変わらない。これらの波は、読み出し勾配磁場 Gx を加えながら取得されたものである。 垂直方向に並ぶ波は、傾斜磁場 Gy を用いた位相エンコーディングによって発生したものである。直交復調によって原データは実数値と虚数値を持っている。位相エンコードのステップ数が 256の場合に垂直 y 方向の位相エンコーディングのエコー信号データは 256の実数のデータ点と 256の虚数のデータ点を持つことになる。したがって、k - スペース上には、256×256の実数のデータ点のセットと 256×256点の虚数のデータ点のセットが存在する。図は実数のデータ点のセットの例である。 
実数値データ Re を k - スペース上で一次元フーリエ変換した結果 図は、k - スペース上に並ぶ実数値データを一次元フーリエ変換した結果である。各横線は 256点からなる折れ線グラフである。ここでも図示していないが、虚数値データを一次元フーリエ変換した結果もこれとは別に存在する。 実数値データと虚数値データを用いて、絶対値 Av データを一次元フーリエ変換した結果を図示する。横線は 256点からなる折れ線グラフで、試料の水平方向のみの情報が可視化されている。縦(y)方向についてはまだフーリエ変換されていない。 
絶対値データ Av = √(Re2 + Im 2)の一次元フーリエ変換結果 k - スペース上にに並ぶ 256×256の実数のデータ点のセットと 256×256点の虚数のデータ点のセットからなる絶対値 Av のデータ点のセットを二次元フーリエ変換した結果を図示する。 
絶対値データ Av の二次元フーリエ変換結果 マトリクスは 256×256のデータ点でできている。横(x)軸の単位は周波数 ω(rad)であり、原点からの距離 [m] に直線的に対応する。縦軸の単位は位相 θ(rad・encoding-steps)であり,同じく原点からの距離 [m] に直線的に対応する。 MRIとは絶対値データの二次元フーリエ変換結果を明度 64諧調以上のグレースケールで表示したものである。 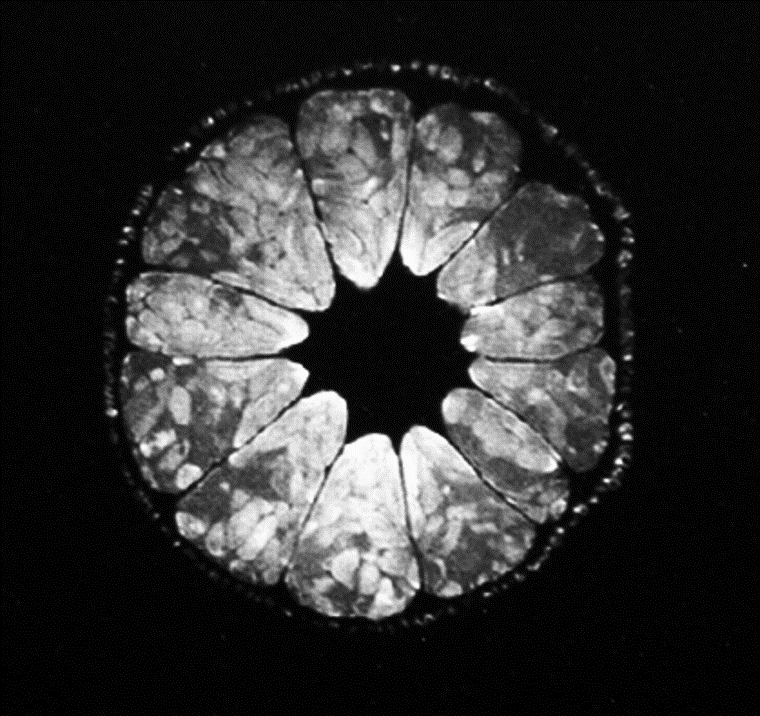
絶対値データの二次元フーリエ変換結果のグレースケール表示 【11】 画像のコントラスト 励起のために RFパルスを印加すると、巨視的磁化ベクトルは z 軸に垂直な成分をもつ。その成分は T2* 緩和によって振幅が減衰する。フィールド・エコー(FE)撮像シーケンスを使用する場合、繰り返し時間 Tr とエコー時間 Te がともに長いと、得られる FE画像は T2* 緩和を反映した T2* 強調画像となる。脳組織の T2* 緩和は脳活動を反映することが多く、ファンクショナルMRI(fMRI)の分野で多用される。スピン・エコー(SE)イメージングでは、磁化ベクトルの z 軸に垂直な成分は T2 緩和によって振幅が減衰する。繰り返し時間 Tr が T1 より長く、エコー時間 Te が T2 より短ければ、得られる SE画像は原子核の所在(密度の分布)を反映する。エコー時間 Te が短いままで、繰り返し時間 Tr を短くすると、T1 が長い試料は T1 緩和が終わらない前に次の励起を受けることとなり、やや小さな信号が取得される。その結果得られる画像は T1 強調画像となり、T1 の分布を反映して、T1 が長い箇所ほど明るい画像となる。繰り返し時間 Tr とエコー時間 Te を共に長くすると、得られる SE画像は T2 緩和の影響を受けたT2強調画像となり、T2 が長い箇所ほど明るい画像となる。フィールド・エコー(FE)画像に比べて SE画像では静磁場の不均一性の影響が少ない。 脳の T1 強調画像では、白質からの信号強度が灰白質より高い。T2 強調画像では、白質より灰白質からの信号強度が高い。 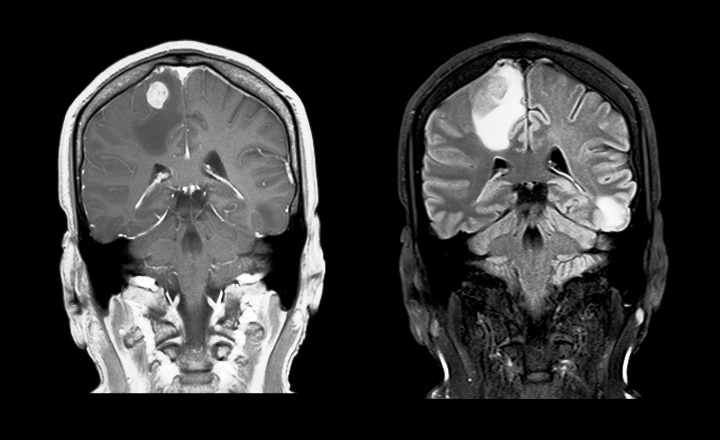
スピン・エコー T1 強調画像 (左)と T2 強調画像(右) 図は、複数の腫瘍病変を有する 46歳男性患者の冠状断 T1 強調スピン・エコー(SE)画像(左)と T2 強調SE画像(右)である。これらの画像は、ドイツの IKR-TRIC大学病院で撮影されたものである(シーメンス社提供)。静磁場(磁束密度)3 [T]、スライス 4 [mm]である。T1 強調画像(左)はマトリクスサイズ 320 の画像である。撮影時間は 84 [s]であった。T2 強調画像(右)はマトリクスサイズ 640 の画像である。撮影時間は 180 [s]であった。図は、同じ患者の横断 T2 強調スピンエコー(SE)画像である。 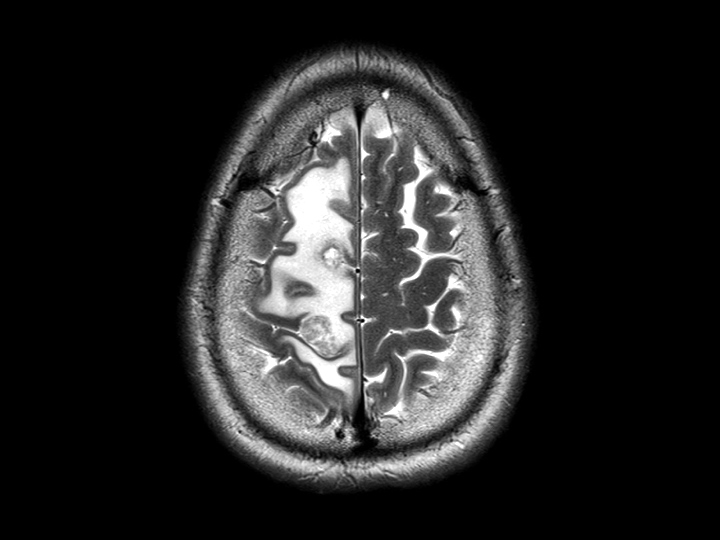
同じ患者のスピン・エコー T2 強調横断画像 【12】 MRI技術の多様化 1.拡散(diffusion)のMRINMRによる拡散の測定は1960年代ごろ始められた[Stejskal, 1965; Stejskal and Tanner, 1965]。水中では、すべての分子がランダムに移動している。細胞の大きさほどの小さな距離をさかんに移動する。これは「ブラウン運動」と呼ばれることが多い。したがって、拡散強調画像は細胞構造の変化を反映する。脳梗塞の組織では、水の拡散が制限され、見かけの拡散係数(ADC)が小さくなる。これは、細胞外腔から細胞内腔へ水が移動することが原因ではないかと言われている[Mosley et al., 1990; Kohno et al., 1995]。傾斜磁場を受けながらランダムに動く原子核は信号を失いやすく、それをMRIで検出することができる。脳梗塞が発症して後数時間以内に得られる病変は T1 強調画像でも T2 強調画像でも分かりにくいが、拡散強調画像では梗塞初期の病変がよくわかる[Mintrovich et al, 1991; Warach et al, 1992; Pennock et al., 1994]。拡散は本来は無方向性の現象であるが、拡散強調画像は、しばしば組織構造の異方性と関連している。この異方性は、傾斜磁場の方向と水の移動による信号損失の程度との関係によって知ることができる[LeBihan and Turner, 1992]。 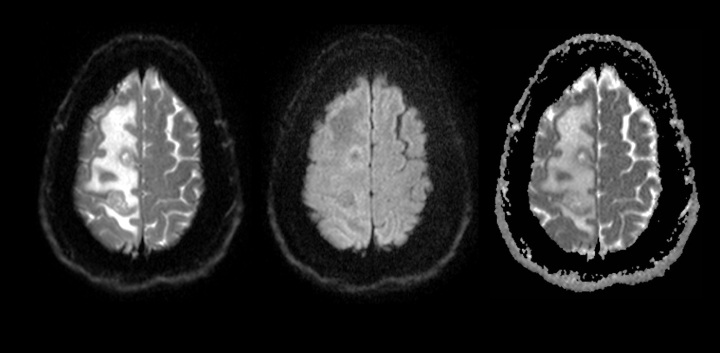
前記患者の拡散強調横断画像(左・中央)と ADC画像(右) 図は前記ドイツの 46歳の男性患者の z 軸方向拡散強調画像(左と中央)とADC画像(右)である。傾斜磁場をどの程度加えたかを表す減衰因子は b = 0(左)、1000(中央)である。 2.ファンクショナル・イメージング(fMRI) ファンクショナルMRI(fMRI)は、脳の活動領域を可視化するものである。
我われの脳内の血液はヘモグロビンをもっている。ヘモグロビン(Hb)は磁性体として鉄 Fe++ の成分をもっている。したがって、脳を貫く静磁場(磁束密度 B0)は脳内では不均一である。したがって、脳からの MR信号は一般に強度が低い(画像が暗い)。これは、血管の外の神経組織からの影響を強く受けている[Ogawa and Lee, 1990; Ogawa et al, 1990; Turner et al., 1991]。脳のある部位が活動すると、その部位の血流が増加してオキシヘモグロビン(Oxy-Hb)が増加する。酸素は磁性体である。その酸素は Hbと結合するとき、Hbの磁性を弱めるように結合する。「血中酸素濃度依存性(BOLD)効果」によって、T2* 強調画像は、活動領域からの信号強度が増加する[Frahm et al., 1992; Bandettini et al.]。fMRIは言語の生成や過去の運動の想起を反映することがある[McCauthyら、1993;Ruechertら、1994;LeBihanら、1993]。fMRIには、典型的には Te = 50 [ms]のフィールド・エコー(FE)イメージング・シーケンスを用いる。
図は、fMRIのルーチン解析画面の一部を示す。複数の関心領域(ROI)に対して同時に解析が行われているところである(シーメンス社提供)。 3.磁気共鳴分光法(MRスペクトロスコピー) 人体の部位を特定して NMRの分析を行う方法である。この MRスペクトロスコピーによって生化学的な変化の初期段階で病変を検出できる大きな可能性がある。水からのプロトン信号は、代謝物からの信号よりはるかに大きいが、水からの信号を抑制することによって代謝物を特定して定量することができる。また、特定の化学物質の代謝物マップや化学シフト画像(CSI)を得ることができる。 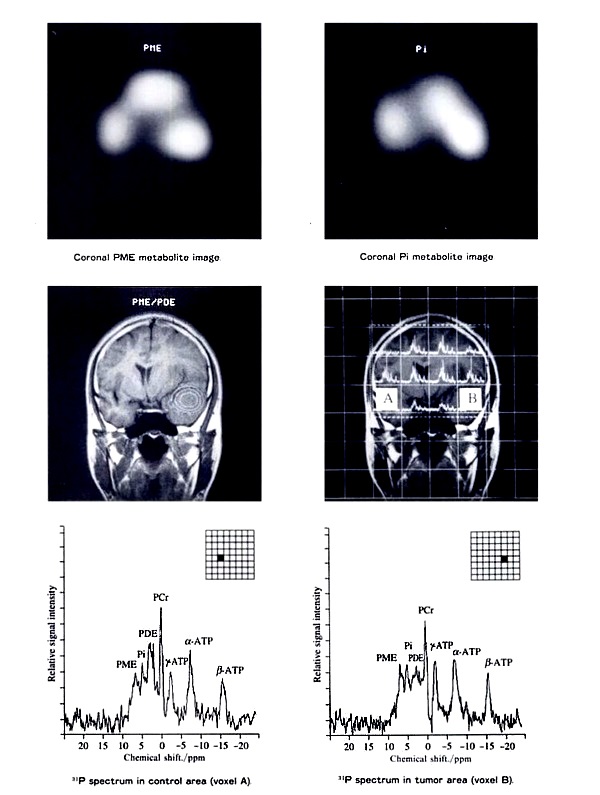
リン(P-31)のスペクトロスコピー画像 (旭化成株式会社 1988年) 5.プロトン以外の原子核のMRI ヒトの腕の自然存在炭素 C-13 MRIは、主に皮下脂肪組織や骨髄の -CH2- 鎖の分布を反映する[Iriguchi and Hasegawa, 1993]。1980年代からアデノシン三リン酸(ATP)、クレアチンリン酸(PCr)、無機リン酸(Pi)の画像 P-31化学シフト画像が得られている。また、重水素(H-2)の MRIやフッ素(F-19)の MRIも行われている。 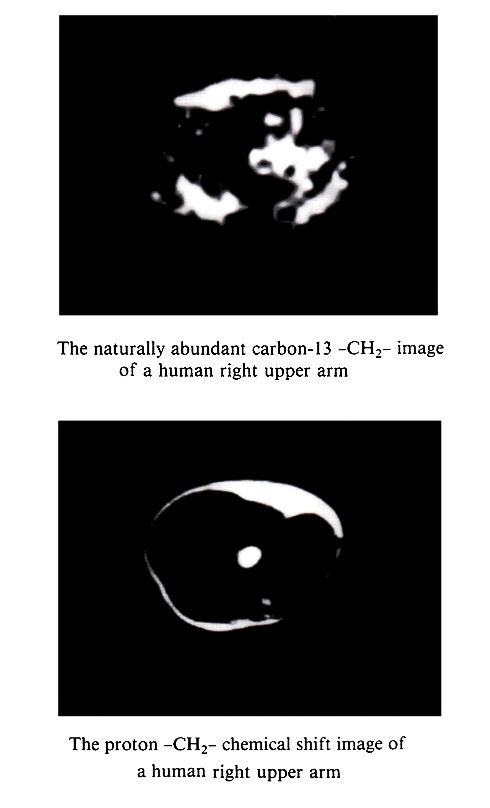
上腕の天然存在 C-13 画像(上)と対応するプロトン -CH2- 鎖画像(下) (旭化成株式会社 1987年) おわりに 前世紀、MRIスキャナー、すなわち磁気共鳴撮像装置は、磁場強度(磁束密度)によって単純に低磁場(0.5T以下)、中磁場(1.0T)、高磁場(1.5T以上)と分類されていた。高性能傾斜磁場コイルの技術進歩によって高品質かつ高速なイメージングが現実のものとなった。現在 MRIスキャナーはより洗練された形で分類されるようになっている。それは、撮像の生産性とリアリティ、臨床現場で使用するための親しみやすい設計コンセプトなどである。基礎技術の分野では、多くの生理学的情報を提供すると同時に、温度、機械的弾性、圧力、電気伝導度、誘電率、代謝物濃度などの物理的、化学的、生物学的な特性を画像化するための技術も開発されている。今世紀もその開発は続くだろう。特に生体などの研究に非侵襲的(non-invasive)な方法を用いることには大きな価値があり、磁気共鳴映像法(MRI)の分野には明るい未来が感じられる。参照文献
|